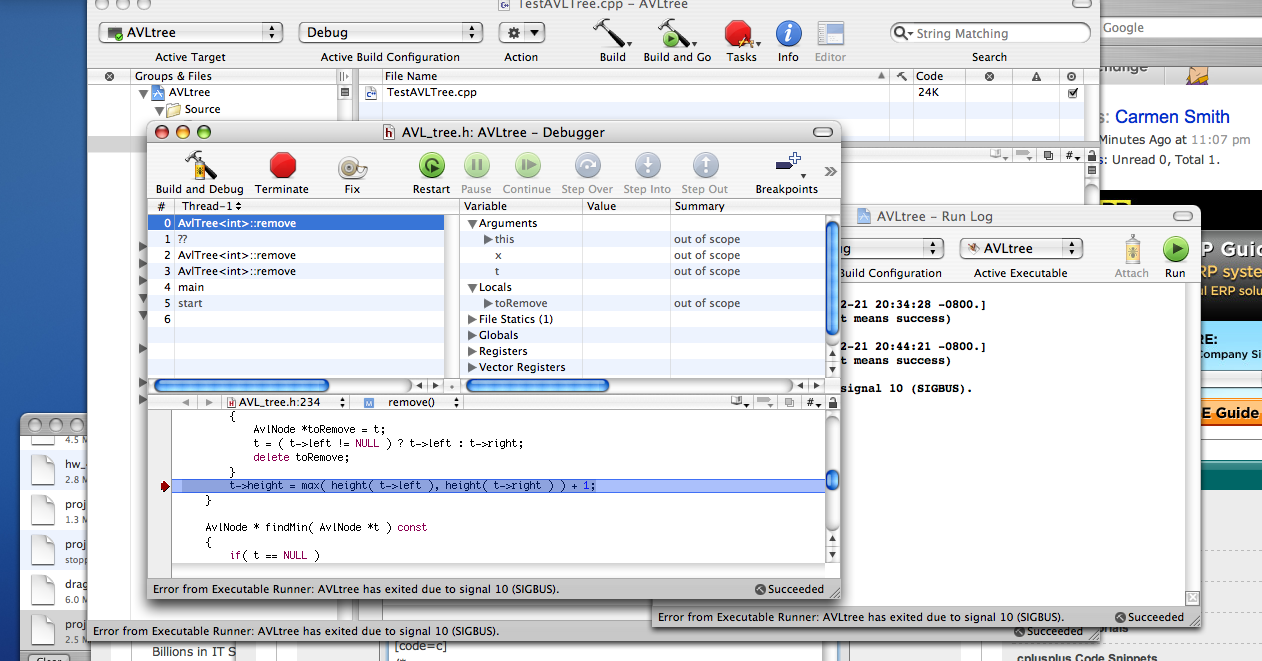
I am having trouble with the remove() function in this avl class. When I run the test below in my main my debugger tells me "there is are not enough frames in stack" pointing to the line
t->height = max( height( t->left ), height( t->right ) ) + 1;Can someone see what my problem is? Thank you in advance!
/*
* TestAVLTree.cpp
* AVLtree
*
*/
#include "TestAVLTree.h"
#include <iostream>
#include "Avl_Tree.h"
using namespace std;
// Test program
int main( )
{
AvlTree<int> t, t2, t3;
int NUMS = 400000;
int testr[6] = {0, 5, 3, 7, 13 };
const int GAP = 37;
int i;
cout << "Checking... (no more output means success)" << endl;
for( i = GAP; i != 0; i = ( i + GAP ) % NUMS )
t.insert( i );
if( NUMS < 40 )
t.printTree( );
if( t.findMin( ) != 1 || t.findMax( ) != NUMS - 1 )
cout << "FindMin or FindMax error!" << endl;
t2 = t;
for( i = 1; i < NUMS; i++ )
if( !t2.contains( i ) )
cout << "Find error1!" << endl;
if( t2.contains( 0 ) )
cout << "ITEM_NOT_FOUND failed!" << endl;
/*** test void remove() ***/
for( i = 0; i < 4; i++ ) t3.insert(testr[i]);
if ( t3.getRoot() == 3)
{
t3.remove(0);
if (t3.getRoot() != 3) { cout << "Remove error, tree has not rebalanced. " << '\n'; }
}
else cout << "error with test remove()!" << '\n';
cout << "Test finished" << endl;
return 0;
}
/*
* AVL_tree.h
* AVLtree
*
*/
#ifndef AVL_TREE_H
#define AVL_TREE_H
#include "dsexceptions.h"
#include <iostream> // For NULL
using namespace std;
// AvlTree class
//
// CONSTRUCTION: with ITEM_NOT_FOUND object used to signal failed finds
//
// ******************PUBLIC OPERATIONS*********************
// void insert( x ) --> Insert x
// void remove( x ) --> Remove x
// bool contains( x ) --> Return true if x is present
// Comparable findMin( ) --> Return smallest item
// Comparable findMax( ) --> Return largest item
// boolean isEmpty( ) --> Return true if empty; else false
// void makeEmpty( ) --> Remove all items
// void printTree( ) --> Print tree in sorted order
// ******************ERRORS********************************
// Throws UnderflowException as warranted
template <typename Comparable>
class AvlTree
{
public:
AvlTree( ) : root( NULL )
{ }
AvlTree( const AvlTree & rhs ) : root( NULL )
{
*this = rhs;
}
~AvlTree( )
{
makeEmpty( );
}
/**
* Find the smallest item in the tree.
* Throw UnderflowException if empty.
*/
const Comparable & findMin( ) const
{
if( isEmpty( ) )
throw UnderflowException( );
return findMin( root )->element;
}
/**
* Find the largest item in the tree.
* Throw UnderflowException if empty.
*/
const Comparable & findMax( ) const
{
if( isEmpty( ) )
throw UnderflowException( );
return findMax( root )->element;
}
/**
* Returns true if x is found in the tree.
*/
bool contains( const Comparable & x ) const
{
return contains( x, root );
}
/**
* Test if the tree is logically empty.
* Return true if empty, false otherwise.
*/
bool isEmpty( ) const
{
return root == NULL;
}
/**
* Print the tree contents in sorted order.
*/
void printTree( ) const
{
if( isEmpty( ) )
cout << "Empty tree" << endl;
else
cout << "root" << root;
printTree( root );
}
/**
* Make the tree logically empty.
*/
void makeEmpty( )
{
makeEmpty( root );
}
/**
* Insert x into the tree; duplicates are ignored.
*/
void insert( const Comparable & x )
{
insert( x, root );
}
/**
* Remove x from the tree. Nothing is done if x is not found.
*/
void remove( const Comparable & x )
{
remove( x, root);
}
/**
* Deep copy.
*/
const AvlTree & operator=( const AvlTree & rhs )
{
if( this != &rhs )
{
makeEmpty( );
root = clone( rhs.root );
}
return *this;
}
bool balanced()
{
return balanced( root );
}
const Comparable & getRoot()
{
return root->element;
}
private:
struct AvlNode
{
Comparable element;
AvlNode *left;
AvlNode *right;
int height;
AvlNode( const Comparable & theElement, AvlNode *lt,
AvlNode *rt, int h = 0 )
: element( theElement ), left( lt ), right( rt ), height( h ) { }
};
AvlNode *root;
/**
* Internal method to insert into a subtree.
* x is the item to insert.
* t is the node that roots the subtree.
* Set the new root of the subtree.
*/
void insert( const Comparable & x, AvlNode * & t )
{
if( t == NULL )
t = new AvlNode( x, NULL, NULL );
else if( x < t->element )
{
insert( x, t->left );
if( height( t->left ) - height( t->right ) == 2 )
if( x < t->left->element )
rotateWithLeftChild( t );
else
doubleWithLeftChild( t );
}
else if( t->element < x )
{
insert( x, t->right );
if( height( t->right ) - height( t->left ) == 2 )
if( t->right->element < x )
rotateWithRightChild( t );
else
doubleWithRightChild( t );
}
else
; // Duplicate; do nothing
t->height = max( height( t->left ), height( t->right ) ) + 1;
}
/**
* Internal method to remove x from a subtree.
* x is the item to remove.
*/
void remove( const Comparable & x, AvlNode * & t )
{
if( t == NULL )
return; // item not found
else if( x < t->element )
{
remove( x, t->left );
if( height( t->left ) - height( t->right ) == 2 )
if( x < t->left->element )
rotateWithLeftChild( t );
else
doubleWithLeftChild( t );
}
else if( t->element < x )
{
remove( x, t->right );
if( height( t->right ) - height( t->left ) == 2 )
if( t->right->element < x )
rotateWithRightChild( t );
else
doubleWithRightChild( t );
}
else if( t->left != NULL && t->right != NULL ) // there are two children
{
t->element = findMin( t->right )->element;
remove( t->element, t->right );
}
else //we have found it
{
AvlNode *toRemove = t;
t = ( t->left != NULL ) ? t->left : t->right;
delete toRemove;
}
t->height = max( height( t->left ), height( t->right ) ) + 1;
}
AvlNode * findMin( AvlNode *t ) const
{
if( t == NULL )
return NULL;
if( t->left == NULL )
return t;
return findMin( t->left );
}
/**
* Internal method to find the largest item in a subtree t.
* Return node containing the largest item.
*/
AvlNode * findMax( AvlNode *t ) const
{
if( t != NULL )
while( t->right != NULL )
t = t->right;
return t;
}
/**
* Internal method to test if an item is in a subtree.
* x is item to search for.
* t is the node that roots the tree.
*/
bool contains( const Comparable & x, AvlNode *t ) const
{
if( t == NULL )
return false;
else if( x < t->element )
return contains( x, t->left );
else if( t->element < x )
return contains( x, t->right );
else
return true; // Match
}
bool balanced( AvlNode *t ) const
{
if( t == NULL )
return true;
/* if any of the subtrees differ by a height greater than 2 then false */
if (( height( t->right ) - height( t->left ) < 2 )) return true;
else return false;
}
bool contains( const Comparable & x, AvlNode *t ) const
{
while( t != NULL )
if( x < t->element )
t = t->left;
else if( t->element < x )
t = t->right;
else
return true; // Match
return false; // No match
}
/**
* Internal method to make subtree empty.
*/
void makeEmpty( AvlNode * & t )
{
if( t != NULL )
{
makeEmpty( t->left );
makeEmpty( t->right );
delete t;
}
t = NULL;
}
/**
* Internal method to print a subtree rooted at t in sorted order.
*/
void printTree( AvlNode *t ) const
{
if( t != NULL )
{
printTree( t->left );
cout << t->element << endl;
printTree( t->right );
}
}
/**
* Internal method to clone subtree.
*/
AvlNode * clone( AvlNode *t ) const
{
if( t == NULL )
return NULL;
else
return new AvlNode( t->element, clone( t->left ), clone( t->right ), t->height );
}
// Avl manipulations
/**
* Return the height of node t or -1 if NULL.
*/
int height( AvlNode *t ) const
{
return t == NULL ? -1 : t->height;
}
int max( int lhs, int rhs ) const
{
return lhs > rhs ? lhs : rhs;
}
/**
* Rotate binary tree node with left child.
* For AVL trees, this is a single rotation for case 1.
* Update heights, then set new root.
*/
void rotateWithLeftChild( AvlNode * & k2 )
{
AvlNode *k1 = k2->left;
k2->left = k1->right;
k1->right = k2;
k2->height = max( height( k2->left ), height( k2->right ) ) + 1;
k1->height = max( height( k1->left ), k2->height ) + 1;
k2 = k1;
}
/**
* Rotate binary tree node with right child.
* For AVL trees, this is a single rotation for case 4.
* Update heights, then set new root.
*/
void rotateWithRightChild( AvlNode * & k1 )
{
AvlNode *k2 = k1->right;
k1->right = k2->left;
k2->left = k1;
k1->height = max( height( k1->left ), height( k1->right ) ) + 1;
k2->height = max( height( k2->right ), k1->height ) + 1;
k1 = k2;
}
/**
* Double rotate binary tree node: first left child.
* with its right child; then node k3 with new left child.
* For AVL trees, this is a double rotation for case 2.
* Update heights, then set new root.
*/
void doubleWithLeftChild( AvlNode * & k3 )
{
rotateWithRightChild( k3->left );
rotateWithLeftChild( k3 );
}
/**
* Double rotate binary tree node: first right child.
* with its left child; then node k1 with new right child.
* For AVL trees, this is a double rotation for case 3.
* Update heights, then set new root.
*/
void doubleWithRightChild( AvlNode * & k1 )
{
rotateWithLeftChild( k1->right );
rotateWithRightChild( k1 );
}
};
#endif