xy-rotation problem

[prushik]

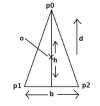
I have a triangle in my game, that flies around the screen (like a space ship)
I am trying to determine collisions for that triangle based on whether or not the lines intersect.
However, I am using OpenGL, so when I rotate this triangle, all I do is make a call to glRotatef(); and it rotates, so I never have to calculate the x,y coordinates. BUT for a line collision check, I need to know the x,y coordinates of all the lines in my triangle.

my triangle is called user

user.x is the x coordinate of the center of the triangle
user.y is the y coordinate of the center of the triangle
user.dir is the direction that the ship is facing

i need to find 3 points: x1,y1, x2,y2, x3,y3

How would I do that?

[prushik]

Ok, I found A solution to my problem, my friend from CISC115 (Computer Science 1) helped me out.
Basically what I do is calculate the distance of the 3 points from the center, and then calculate the direction from the center point. Then all I have to do to find the points after rotation is use trig functions (sine and cosine) after I add the rotation of the entire triangle to the angles i calculated before (multiplied by the distance)

float  dir1,dir2,dir3;
     double d1,d2,d3,
            x1,x2,x3,
            y1,y2,y3;
            
     d1=sqrt((user.x+15)*(user.x+15)+(user.y)*(user.y));
     d2=sqrt((user.x-10)*(user.x-10)+(user.y-10)*(user.y-10));
     d3=sqrt((user.x-10)*(user.x-10)+(user.y+10)*(user.y+10));
     
     dir1=atan2(0,15);
     dir2=atan2(-10,-10);
     dir3=atan2(10,-10);
      
     x1=(user.x)+(cos((user.dir+dir1)*(PI/180)))*(d1);
     x2=(user.x)+(cos((user.dir+dir2)*(PI/180)))*(d2);
     x3=(user.x)+(cos((user.dir+dir3)*(PI/180)))*(d3);
     y1=(user.y)+(sin((user.dir+dir1)*(PI/180)))*(d1);
     y2=(user.y)+(sin((user.dir+dir2)*(PI/180)))*(d2);
     y3=(user.y)+(sin((user.dir+dir3)*(PI/180)))*(d3);

[prushik]

Ok, I found A solution to my problem, my friend from CISC115 (Computer Science 1) helped me out.
Basically what I do is calculate the distance of the 3 points from the center, and then calculate the direction from the center point. Then all I have to do to find the points after rotation is use trig functions (sine and cosine) after I add the rotation of the entire triangle to the angles i calculated before (multiplied by the distance)

float  dir1,dir2,dir3;
     double d1,d2,d3,
            x1,x2,x3,
            y1,y2,y3;
            
     d1=sqrt((user.x+15)*(user.x+15)+(user.y)*(user.y));
     d2=sqrt((user.x-10)*(user.x-10)+(user.y-10)*(user.y-10));
     d3=sqrt((user.x-10)*(user.x-10)+(user.y+10)*(user.y+10));
     
     dir1=atan2(0,15);
     dir2=atan2(-10,-10);
     dir3=atan2(10,-10);
      
     x1=(user.x)+(cos((user.dir+dir1)*(PI/180)))*(d1);
     x2=(user.x)+(cos((user.dir+dir2)*(PI/180)))*(d2);
     x3=(user.x)+(cos((user.dir+dir3)*(PI/180)))*(d3);
     y1=(user.y)+(sin((user.dir+dir1)*(PI/180)))*(d1);
     y2=(user.y)+(sin((user.dir+dir2)*(PI/180)))*(d2);
     y3=(user.y)+(sin((user.dir+dir3)*(PI/180)))*(d3);

HOWEVER, it seems to me that this is a rather sloppy way of doing things....
I do not like sloppy. Does anyone know of a better method?

[MattEvans]

You don't need all the trig stuff, but the principle is OK. See attached diagram for a guide to what each variable in these expressions is. Assuimg your triangle is isocoles; and is defined as having a base ( scalar ), height( scalar ), origin/centerpoint ( point ) and direction ( vector ).

ASIDE: the first thing you should do when using OpenGL is to write or obtain a library for basic vector and matrix operations; it will make your life a lot, lot easier if you do so. See the dif between the vector implementation and component-wise implementation given.

VECTORS:

Given, origin = o, direction = d, base = b and height = h:

  d_n = normalize( d )
  pd_n = perp( d_n )

  p0 = o + ( d_n * (h/2) )
  p2 = o - ( d_n * (h/2) ) + ( pd_n * (b/2) )
  p2 = o - ( d_n * (h/2) ) - ( pd_n * (b/2) )

NOTE: the vector operations normalize and perp will be provided by any math/vector library worth mentioning, they are shown in full in the component method below, though.

COMPONENTS:

Given, origin = o, direction = d, base = b and height = h:

  // this is how normalization looks component-wise
  d_l = sqrt( (d[x]*d[x]) + (d[y]*d[y]) )
  d_n[x] = d[x]/d_l
  d_n[y] = d[y]/d_l
  
  // this is how perp(endicular) looks component-wise
  pd_n[x] = d_n[y]
  pd_n[y] = -d_n[x]

  p0[x] = o[x] + ( d_n[x] * (h/2) )
  p0[y] = o[y] + ( d_n[y] * (h/2) )

  p1[x] = ( o[x] - ( d_n[x] * (h/2) ) ) + ( pd_n[x] * (b/2) )
  p1[y] = ( o[y] - ( d_n[y] * (h/2) ) ) + ( pd_n[y] * (b/2) )

  p2[x] = ( o[x] - ( d_n[x] * (h/2) ) ) - ( pd_n[x] * (b/2) )
  p2[y] = ( o[y] - ( d_n[y] * (h/2) ) ) - ( pd_n[y] * (b/2) )

This wont compile in any language; it's just a pseudocode example - to make it 'C' just take out the square brackets ( unless you're using arrays for points ), add semicolons, include <math.h> for sqrt, declare the variables... etc.

IMPORTANT: this will ONLY work for 2D movement, crucially, 2D rotation - because the 'perp' method is only really well defined for 2D vectors. If you're doing this in 3D, you should use 4x4 matrices to represent the transform of your ship - and then it is easy: multiply the centered ( original ) points of the triangle with the transform matrix for the ship at any point in time; and the results will be the points in the correct place at that time. This looks pretty much like what your friend is doing in the example you gave; except it is in full component-wise calculations: again this is much easier to do yourself if you write/obtain a matrix library. Alternatively; if in 3D, you can provide a 'direction' and a 'roll ( left wing direction )' vector; put the normalized roll instead of the perp( direction ) in these calculations.

[prushik]

Wow, ok. Thank you very much

[rick222]

I think there is something wrong in the codding ...make sure that its correct...

[MattEvans]

You're right rick. There is an error. In the vector method; there are two lines that assign to 'p2'. One of those should assign to 'p1' ( it doesn't matter which, but, it will affect CW/CCW winding of the points in the triangle ).

d_n = normalize( d )
  pd_n = perp( d_n )

  p0 = o + ( d_n * (h/2) )
  [b]p1[/b] = o - ( d_n * (h/2) ) + ( pd_n * (b/2) )
  p2 = o - ( d_n * (h/2) ) - ( pd_n * (b/2) )

Otherwise; both the vector and component method work fine, after converting into C code. ( I have just checked )