Detecting the point of collision between a rotating point and a rotating line.

[Konokai]

I'm trying to formulate an algorithm that will calculate the point where an independently rotating point collides with an independently rotating line.This will only concern instances where the rotating point, which will be called P1 from now on, and the rotating line, which will be called L1 from now on, are rotating in a two-dimensional plane where the axes of rotation for both P1 and L1 are parallel. L1 will also be expressed as two rotating points, P2 and P3, around the same point of rotation.

Both the systems associated with P1 and L1 will have the following known values:
w - The angular velocity of each system, expressed in degrees/frame.
r - The distance to each system's point of rotation, expressed in pixels.
(cx,cy) - The coordinates of the point of each system that is being rotated around
(P1.x,P1.y)... - The coordinates of P1,P2, and P3 when the systems are at their final state.
O° - The angle to the rotating point, P1, from C1, which is the point of rotation in the system that deals with P1. It is also the angle to the point on the rotating line, P2, from C2, which is the point of rotation in the system that deals with L1.
w2/w1 - The ratio of the angular velocities of each system. It will be assumed that w1 > 0. w2 is the angular velocity of the system that deals with L1, and w1 is the angular velocity of the system that deals with P1.

The point where P1 collides with L1 is where the angle to P1 from P2 is the same as the angle to P3 from P2. Here's an example to further explain what I mean.

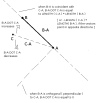
http://i129.photobucket.com/albums/p231/Konokai/Picture.png
* cw = clockwise and will be expressed in negative degrees
* ccw = counter-clockwise and will be expressed in positive degrees

There are three pictures of two objects rotating. The red circle on the left shows the system that deals with P1, and the green circle on the right shows the system that deals with L1. L1 is the line segment that connects P2 and P3 together. The initial state shows the starting position of each point before they are rotated. The intermediate state shows the position of P1 and L1 after they each have half of their angular velocities added to the angle to each point from the point of rotation of each system (C1 and C2). This is also where P1 intersects L1, as the angle to P1 from P2 is the same as the angle to P3 from P2, which is 0°. The final state is what is shows after the total angular velocity is added to each system. As you can see, P1's orientation is 180° different from its initial state, and P2's and P3's orientations are 90° different from their initial states. Also, the coordinate system in this example mimics the coordinate system found in most computer programs, where the top-left corner is the origin and the value of the y-axis increases as you move downwards.

The only state the program will be able to detect is the final state, and since all of the factors that dictate where the point of collision occurs are known, it should be possible to find a function to give that point. A way to find that point is to simply know how much, in degrees, that P1 needs to "back up" in order to be in the orientation where it collides with L1. This value will now be known as F°.

In the above example F° = 90°,as that is the amount needed to "back up" P1 to be in the same position as it is in the intermediate state where the collision happened. To find the corresponding angle for L1, just multiply the ratio of the angular velocities of each system by F°. In the above example, the ratio is -1/2 (w2/w1 = 90/-180 = -1/2), so the corresponding angle would be -45° (w2*F°/w1 = 90*90/-180 = -45°).

The problem is finding a way to find F°. The means to find F° must include each systems' angular velocities(w1 and w2), position of the points of rotation(C1 and C2), final state orientation (O1° and O2°), radius from P1 and P2 to the points of rotation (r1 and r2). Another value, the offset added to the angle to P2 from C2 to find the angle to P3 from P2, which will be known as K°, must also be known. In the final state in the above example, K° = 180° as you need to add 180° to the angle to P2 from C2 to get the angle to P3 from P2 (O2° = 225°, angle to P3 from P2 = 45°, 225° - 45° = 180°. To check if this is right, O2 + K = angle to P3 from P2, 225° + 180 = 405° - (360°) = 45°, so this is right).
The position that P1 will be when the collision occurs will be the ordered pair (x1, y1), and the position that P2 will be when the collision occurs will be the ordered pair (x2, y2). The angle between these two points must be the same as the angle to P3 from P2 when the collision occurs, which can be expressed as (O2 + w2*F°/w1) + K°. (O2 + w2*F°/w1) will find what O2 was when the collision occurred, and adding the offset, K°, to that value will get the angle to P3 from P2 when the collision occurred.
To find the angle between two points, you must subtract the coordinates of the point that will be used as the origin, P2, from the point you want to find the angle to, P1, and then use these values in the inverse of the tangent function. These two values will be known as simply x and y.

To clarify...
arctan(-y/x) = (O2 + w2*F°/w1) + K
where
y = y1 - y2
x = x1 - x2
(y is multiplied by -1 to correct the fact that we are working in a computer-based coordinate system)

The arctan function is not accurate at all times, and some rules needed to be combined with the result in order to get the correct angle between the two coordinates. In the above example, however, these rules do not need to be applied.

(x1,y1) and (x2,y2) can be expressed as follows:
x1 = cos(O1 + F°) * r1 + C1x
y1 = -sin(O1 + F°) * r1 + C1y

x2 = cos(O2 + w2*F°/w1) * r2 + C2x
y2 = -sin(O2 + w2*F°/w1) * r2 + C2y
(sin is multiplied by -1 to correct the fact that we are working in a computer-based coordinate system)
(C1x means the x-coordinate of C1, C1y means the y-coordinate of C1, etc..)

Using the above example, we will use this method to show that P1 and L1 collide when we substitute the variables needed with the values found in the final stage and with the already-known information that F° = 90°.
Using the information given in the final stage...
O1 = 270°, O2 = 225°
w1 = -180°, w2 = 90°
r1 = 50, r2 = 50
C1 = (50,50), C2 = (137.5,50)
angle to P3 from P2 = 45°
K° = O2 - angle to P3 from P2 = 180°
F° = 90 (Already known given the example. In other problems this value is not known but needs to be found. The method to find this is unknown, and it is the reason I'm posting all of this in the first place.)

Using this information to see if it works...
x1 = cos(O1 + F°) * r1 + C1x = cos(270° + 90) * 50 + 50 = 100
y1 = -sin(O1 + F°) * r1 + C1y = -sin(270° + 90) * 50 + 50 = 50

x2 = cos(O2 + w2*F°/w1) * r2 + C2x = cos(225° + 90*90°/-180) * 50 + 137.5 = 87.5
y1 = -sin(O2 + w2*F°/w1) * r2 + C2y = -sin(225° + 90*90°/-180) * 50 + 50 = 50

x = x1 - x2 = 100 - 87.5 = 12.5
y = y1 - y2 = 50 - 50 = 0

O2 + w2*F°/w1 + K = 225° + 90*90°/-180 + 180° = 360° = 0°

arctan(-y/x) = arctan(0) = 0°

arctan(-y/x) = O2 + w2*F°/w1 + K = 0°
Since the above statement is true, P1 collides with L1 when P1 is "backed up" by 90° and when P2 is "backed up" by -45° (w2*F°/w1 = 90*90°/-180 = -45°).

The problem is that I don't know how to turn the equation (arctan(-y/x) = O2 + w2*F°/w1 + K = 0°) into a function that will return F°. F° is found on both sides of the equation, and when you factor in the rules that need to be applied to arctan to find the real angle when given any two points, it seems pretty impossible.

I realize that no one will read this whole thing completely understanding what I'm saying, and I apologize sincerely for this. I've tried very hard to express this problem in the clearest way that I could, but I don't think I'll get an answer anytime soon. If you actually know what I'm talking about, please let me know how you would approach this problem. If you know some genius that can solve any mathematical problem, please let me know this person so that I can contact him/her. If you know of a forum that exists somewhere else on the internet that handles problems like this, it would be very nice to show me the link to such a place. Thank you in advance.

[MattEvans]

I don't have a complete answer to this, ( not a mathematical genius! ), but you said you wanted to hear how people might go about this.. and the following is how I'd start:

assume:

ax, ay = rotation origin for the point
ar = initial rotation of the point
ad = distance of the point to its rotation origin
av = angular velocity of the point

for the line segment, I'd temporarily treat it as an infinite line passing through its own rotation origin and through another point, which I'll define as b ( with same attributes as the point a ). If the systems are as in the image you depicted, it seems like it should be sufficient to work out whether or not the point intersects the infinite line; if the intersection is within the line segment, then it's a collision, otherwise, the objects will never collide...

.. incidently, in this setup, the two objects will either never collide, or will collide an infinite number of times. I guess that you want the smallest positive time at which the objects will collide, this can then be multiplied by the angular velocity to work out where the objects are.

now... collision between an infinite line through the points L0 and L1 and another point P occurs when:

(P-L0).(L1-L0) = 0
[ where . is the vector dot product ]

the actual position of the point P at any time ( t ) is given by:

x = (ax+ad*cos(ar+t*av))
y = (ay+ad*sin(ar+t*av))

similarly for L1:

x = (bx+bd*cos(br+t*bv))
y = (by+bd*sin(br+t*bv))

and for L0:

x = bx
y = by

and, given ( A DOT B ) = ( Ax * Bx + Ay * By ) that expands to the somewhat ugly:

{[(ax+ad*cos(ar+t*av))-bx]*[(bx+bd*cos(br+t*bv))-bx]}+{[(ay+ad*sin(ar+t*av))-by]*[(by+bd*sin(br+t*bv))-by]} = 0

and you'll want to find the roots ( solve for t ) given an ax,ay,ad,av,bx,by.. etc.. but, unless I'm missing something, you can't do this in an 'easy', analytic way.

the same kind of thing ( arranging to find the first time of collision by solving an equation containing the definitions of the moving objects ) usually works well in situations where objects are undergoing linear movement ( translation ) but rotation.. is nasty. certainly for general 2d ( or 3d ) shapes, it's pretty much impossible to analytically find the time of collision when both objects are rotating at different rates and/or on different axis, but I would of thought it possible with just simple lines and points on the same axis {{ by the way, I do believe the equation above CAN be simplified and perhaps solved analytically if one of the objects isn't rotating, or if both objects rotate at the same speed. }}

... you can use trigonometric identities to simplify the cos(a+b) and sin(a+b) type sub-expressions.. but not to remove the cos(a*b) or sin(a*b) expressions, this is what makes it difficult.. an alternative might be to perform a 4-term taylor expansion equiv. of cos and sin, but then you have to solve an equation with two independant 7-degree polynominals.. and I don't even know if that's feasible.

since the LHS of the function i just posted plots out a vaguely sinusoidal curve that either touches 0 or doesn't, another alternative would be to use a general root-finder to try and solve it... finding the the first point where the curve's gradient changes from pointing towards y=0 to pointing away from y=0 is a sufficient termination condition ( since the curve seems periodic ).

I'll have a bit more of a think about it, and post back if I have any ideas ( or perhaps corrections to what I've just said =P ), but, no promises that I'll be able to come up with/find out anything more, and also no guarantee that the method I've suggested is the best way to go about it.

[MattEvans]

heh, dumb mistake, the line and point collide when:

( NORMALIZE (P-L0) DOT NORMALIZE(L1-L0) ) = +1
..or..
( NORMALIZE (P-L0) DOT NORMALIZE(L1-L0) ) = -1

for a segment, leave out the -1 case, you still need inclusion checking afterwards, and I think you'd need at least two roots, since the line might touch the point as it rotates on the other side of it's "circle", and that might fall outside the segment.

that makes the expansion alot more ugly. expanding with acos / atan ( similar to how you're going about it ) would also require the normalization, and is unecessary when only checking for the angle 0..

if you use a general root finder, the complexity of the expression isn't a problem ( although the time taken to solve might be )

[MattEvans]

Actually, the first equation I gave wasn't so far wrong. In case your not sure what I'm suggesting, I've attached an image showing the 'reason' why the first equation is wrong, and the second is 'more right'.

The vector from the moving point to either of the line's defining points can be used to determine whether or not the line and point intersect, since when acos(A DOT B) = 0 ( i.e. when the angle is zero ) the argument must be 1. Thus, you can skip the evaluation of the acos, and/or write a formula to determine whether or not the argument approaches 1.

You can also avoid the normalization of the two vectors. In the attached image, it can be seen that working out whether or not the angle between the point and the line is zero is more difficult than working out if the angle between the parallel line that passes through the first line endpoint is zero, since when the dot product is zero, the vectors are perpendicular irrespective of their lengths. Thus, rather than try and incorporate the length between A and C ( which changes with respect to time ) in an equation, you can simply check if the dot product between that perpendicular and the vector between the point and the line startpoint reaches zero.

For finding a perpendicular vector to a given vector in 2d:

perp ( x, y ) = [ -y, x ]
..or..
perp ( x, y ) = [ y, -x ]

And, for that to work even close to pleasantly in the context of an equation, it'll be easier to shift everything into the co-ordinate frame of the first point of the line..