Convert mouse position to Texture position on ball

[3DStarter]

Hi All,

I am an experienced Java developer and since a few weeks I joined a project which involved real time rendering of 3D objects and interaction with those objects. I have a problem for which I hope that an experienced 3D programmer can help me. Usage:

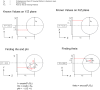
• I’ve rendered an 3D Sphere object which in this case is a perfect ball (not eggs shape) using Spherical Texture mapping.
• The idea is that a user can interact with this ball and rotate the ball. The user clicks a location on the ball and the user is to enter a ‘dot’ on the ball. Thereafter the user can rotate the ball and place other dots on the ball.

Problem statement

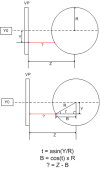
1. When a user clicks the surface of the ball our application is able to get the mouse position (x, y) in Canvas2D.

Question: How can I convert the mouse position to the Texture position in order to update the ball surface?

If you are able to help or if you need more information please let me know because I am really stuck with this.

Martijn Hermanns

[iamthwee]

Ok kiddo, what api are you using?

JOGL or java 3d?

How much of this have you read.

Have you been through the tutorials?

[3DStarter]

I read a lot but haven't found a solution for my problem so far. Please instruct me if there are any tutorials which could meet my problem.

The problem is that we have to rotate the ball and that is where I get lost.

[iamthwee]

Ok, first of all I'd use the JOGL api. It looks good.

Then I'd work throught the NeHe tutorials. Fortunately, some kind soul has ported them to JOGL.

Read this

[iamthwee]

Have a look at this as well.

It's a basic java program that rotates a wireframe object in 3d space.
All you have to do is provide the coordinates of the model. (Source code provided)

Just make sure you unzip the file after downloading it. (Right -clicked the folder icon and select extract all)

[IMG]http://img136.imageshack.us/img136/5761/oirz8.th.gif[/IMG]

[3DStarter]

thank you for responding. We will have a look at the link you provided to and hope to find the answer to the solution.

Unfortunately the weee.zip sample does solve our problem because it simply rotates a sphere when user the user drags the mouse. I really need to know "How can I convert the mouse position to the Texture position in order to update the ball surface?".

[iamthwee]

I think the best way to do this is to download the JOGL stuff and work with some of the tutorials. Then you can apply the texture mapping in a 3d environment.

The mouse listeners should be no different to the ones you use for any other bog standard java application. It's just the texture gets updated straight away.

Try it.

[3DStarter]

Maybe you misunderstand my problem. Converting coodinates after applying texture mapping is not the same as simply applying texture mapping.

I see that Zaknixon got the same problem but couldn't find a proper feedback in JOGL forum.

http://www.javagaming.org/forums/index.php?topic=1595.0

Can you please clarify?

[MattEvans]

If you were only using a circle, not a sphere, it's simple trigonometry; sphere is abit more difficult though, do you have to take rotation (of the sphere) into account?

For a circle though; see attached image, and you must know:

- The distance (D) from the viewing platform to the center of the object
- The distance (Y) from the line Y=0 (relative the sphere AND viewing platform) to the point where the click is received from.
- The radius (R) of the object.

This won’t work directly with spheres, it assumes a cylindrical object lateral to the viewing platform, with a zoom factor of 1, and no transformations.

The point you’ll get is X,Y,Z where (X,Y) are the clicked co-ordinate, and Z is the result of:

t = asin(Y/R)
B = cos(t) x R
Z = D – B

If the X and Y values are within a distance (the object’s size as centred around the line X = 0, Y = 0) from the point X = 0, Y = 0; then the point is on the surface of the object, at the point X,Y,Z relative to the viewing platform.

To map that to a texture co-ordinate is different, it depends on your texturing system/method of creating the object; you can find the point relative to the object as opposed to relative to the viewing platform by subtracting the value of Z from the value of D, or taking the initial value of B.

Taking that from a circle function to a sphere function could be simple, but could be difficult depending on the potential for/possibility of rotation, particularly if it's about arbitrary axes.

Hope that helps; but definately try looking for third party packages/extensions that implement point picking; there may be some in Java3D already somewhere, look in the Java3D examples folder, I remember seeing some nice picking demos in there.

Another solution (if texture point picking isn't implemented) is to put objects (which CAN be picked easily using the mouse) at every texture point, store reference to the texture point in that object, catch the pick with a behaviour and mutate or return the reference depending on what kind of app you're making.

Matt

[3DStarter]

Hi Matt,

Thank you for the detailed explanation. Assuming that the convert formula

t = asin(Y/R)
B = cos(t) x R
Z = D – B

is correct this would answer a part of the problem. This only converts from Canvas coordinates (x, y) to Virtual World coordinates (x, y, z). How about convert from Virtual World coordinates (x, y, z) to Spherical coordinates (rho, phi, theta) and to Texture coordinates (u, v).

Do you have any idea on that?

[MattEvans]

it actually only converts a Y to a Z (2D), the value of Z also has to be in terms of the X to be a sphere; to convert them to a spherical system, rho will equal Z, phi will equal Y, and theta will be in terms of Z and X, the sphere co-ordinates and/or mapping to UV depend on the rotation, translation and scale of the sphere at any moment in time.

EDIT: no, rho will equal (distance from sphere to viewing platform) - Z, and phi will equal the distance from the Y origin of the viewing platform to the Y co-ordinate (as clicked on the Canvas)

do you have the java3d demos? look for ..\jdkx.x\j3d\demo\index.html and check out, PickTest and IntersectTest. These methods work by flagging collisions as the graphics are rendering as opposed to calculation positions from current transform3d objects.

Intersect test is quite good, shows picking of points rather than objects.

[3DStarter]

Hi Matt,

Thanks again. We will try to implement the OpenGL document in Java3D.

Assuming that there are no rotation (dx=0; dy=0; dz=0), no translation (dx=0; dy=0; dz=0), no scale (=1.0) at that time, could you please provide the formula for computing U,V?

Terms
See the document: http://www.opengl.org/resources/code/samples/sig99/advanced99/notes/node177.html
(This document is written for OpenGL sp it may be easier to implement in JOGL however we prefer Java3D because Java3D code could work in OpenGL and DirectX, meanwhile JOGL code doesn't work in DirectX)

Some terms I don't understand:

1. "The vector from the eye point to the vertex". How to get this in Java3D?
2. "The modelview matrix". How to get this in Java3D?

As always you feedback is much appreciated.

[MattEvans]

I've attached a new image showing how to get rho,phi and theta values on a sphere; bear in mind these equations have only been tested mentally, so look carefully at the proofings. You may find that some of the axes are expressed upside down, that's a common mistake I make.

You'll notice that there's no longer a Z (distance from viewplatform (eye) to the surface of the circle) in terms of the Y and Z (that is; origin-to-origin displacement Z). It's no longer calculatable by those terms as it was before because the theta value (well, third dimension) affects that distance.

Once you have these; converting them to UV is dependant on your system of mapping UV co-ordinates to rho, phi and theta values. I'm assuming that you derive the UV co-ordinates from rho, phi and theta values, and in that case it'll be easy. I can't tell you how; because UV isn't finite/has no referenceable standard that I know of.

On your sphere, the vector from the eye point to the matrix is the vector from the origin of the camera/viewplatform to a vertex on a shere as it would be if it were a point in global space (so after rotation, scale etc), bear in mind the vertexes location is not the UV co-ordinate.

The modelview matrix is a mixture of the transform matrix * of a model and the transform matrix of the viewplatform/camera/eye. If the object is never moved but the eye is moved, the modelview matrix is the transform matrix of the eye; and if the object is moved and the eye is never moved, it's the INVERTED transform matrix of the object. If both are moved; it's the composite of the camera transform matrix and the inverted model transform matrix. There may be some kind of combine in the Transform3D class, I've never used it, I usually do all parts of 3D transforms separately and build Transform3D's ad-hoc.

* Call getTransform() of a TransformGroup object to access it, but if you're scenegraph/locale is compiled, you'll need to set the ALLOW_TRANSFORM_READ (and probably ALLOW_TRANSFORM_WRITE) capabilities of the transformgroup/object in question.

Looking at the class functions in JBuilder, it'd probably be:

Transform3D modelMatrix = new Transform3D();
model.getTransform(modelMatrix);
modelMatrix.invert();
 
Transform3D viewMatrix = new Transform3D();
view.getTransform(viewMatrix);
 
 
Transform3D modelViewMatrix = new Transform3D(viewMatrix);
modelViewMatrix.add(modelMatrix);

I think I've earnt the right to tactlessly promote my own forum, so check it out: http://www.fusiongroupuk.com. I will post some topics/tutorials about 3D and Java3D there sometime. There'll definately be 3D programs, and maybe some textures and models if I can enlist my lil brother's help :) there's not much now though, but check out the demos in the ElementSystem board. It makes me proud :mrgreen:

Good luck, let me know if you have any trouble (especially if you get the equations in and they do something unexpected).

Matt

[MattEvans]

there's at least one mistake in the diagram; the line labeled "rho" is actually not rho; you need to calculate the length of that line to work out phi, so rename the line rho on the diagram to the line B.

rho now is equal to the "radius" and is constant for all values that fall on the sphere's surface.

[3DStarter]

Hi Matt,

I am terrible sorry that I didn't reply earlier. Indeed you have well earnt the right to tactlessly promote your forum.

Your feedback is a great help. We are now working based on the information you provided and will let you know how we get on with it.

Thanks again,
Martijn

[3DStarter]

Hi Matt,

Good news. Thanks to your input all is working correctly.

Thanks a lot for your help,
Martijn

[3DStarter]

Hi Matt,

Good news. Thanks to your input all is working correctly.

Thanks a lot for your help,

Martijn