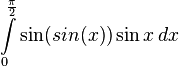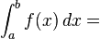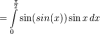Simpson's rule

[Auroch]

Hello. I need to write a program to evaluate a definite integral with Simpson's composite rule.

1. 

I know there is a Simpson's rule available in Scipy, but I really need to write it by the following scheme.

1. ,

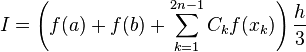where a, b - limits of integral, n-number of intervals of integral's partition.

1. 

for k-even
and

1. 

for k-uneven

I already got this far (see below), but my answer is not correct. The output of my code is equal 0.07. But answer of WolphramAlpha that uses identical algorithm is 0.439818.

Click Here

(WolframAlpha result)

What should I change for in my code? Any help will be appreciated.

#include <iostream.h>
#include <math.h>
#include <conio.h>

using namespace std;

double f(double x) {
    return ((0.6369)*sin(sin(x))*sin(x));
}

int main() {


double a = 0.0;
double b = 1.57;
double n = 2.0;
double eps = 0.1;

double h = (b-a)/(2*n);
double s = f(a) + f(b);
int k = 1;
int x;
double i;

while (k>(2*n)-1) {
    x = a+h*k;
    s = s+4*f(x)+2*f(x+h);
    k = k+2;
    }

i = s*h/3;

cout << "integral is equal " << i;
cout << "\nPress any key to close";

getch();
return 0;
}

[mike_2000_17]

I think it's a simple typo. You have while (k>(2*n)-1), I think that it should be while (k < (2*n)-1), notice the less-than instead of greater-than.

You might also notice that using more spaces between things will help you find such errors. It's easier to spot a typo like this in while ( k > (2 * n) - 1 ) than it is to find it in while (k>(2*n)-1).

Also, your code is not standard C++. You use the pre-standard header "iostream.h", the C header "math.h", and the non-standard header "conio.h". In standard C++, the first include statement should be #include <iostream>, the second one should be #include <cmath> (the C++-friendly version of the C header "math.h"), and the last one should not be there at all, because it is a platform-specific header (and not widely supported anymore, because it's so old, from the DOS era). To replace the getch() call (which is from conio), you can use this code which is more or less equivalent:

char c;
cin >> c;    //<-- equivalent to 'getch();'

[Auroch]

Oh, it's necessary to change condition while (k<n). Now answer is equal to 0.09. It's a bit better but not correct.

[mike_2000_17]

Well, another problem is that "n" should be an integer, not a double. When you evaluate the expression (2*n)-1 you get 3, but if "n" is a double variable, then that "3" might actually be "2.9999.." or "3.000001", which changes things a bit, obviously. So, declaring "n" as an integer should help, i.e., with int n = 2;.

Also, I think that the less-than < in the loop condition should actually be a less-than-or-equal <= condition. With n = 2, you have 2*n-1 = 3, and you are starting with k = 1, which is then incremented by 2, giving you k = 3, which will terminate the loop (before a second iteration can occur) because 3 is not less than 3.

Another issue that you have there is that the last point in the intervals is being counted too many times (it's added up 3 times, but should be added only once). With the Simpson's rule, for n = 2, you should have the following sequence of coefficients between a to b:

a   a+h  a+2h a+3h  b
1    4    2    4    1

But with your current implementation (after making n an integer and fixing the condition to <=), you will get the following sequence of additions to the "s" sum:

just before entering loop:
a   a+h  a+2h a+3h  b
1    0    0    0    1

after first iteration (k=1) in loop:
a   a+h  a+2h a+3h  b
1    4    2    0    1

after second iteration (k=3) in loop:
a   a+h  a+2h a+3h  b
1    4    2    4    3

Basically, you count the last point as if it was a middle point between two intervals, but it's actually the end-point, which you have already taken into account before the loop. One way to fix this is to simply do this:

double s = f(a) - f(b);

So that when you get to the last iteration of the loop, you will add 2 times the last value, which has already been subtracted once from "s", which gives you a net result that it only appears 1 time in the final sum.

BTW, a much easier way to calculate Simpson's rule is to use the sum in the right-hand-side of this equation.

[Maritimo]

The analitical answer is 0.440244, so this is the limit that you must arrive with a lot of intervals.

Here you have your code modified to the right answer:

#include <iostream>
#include <cmath>

using namespace std;

double f(double x)
{
  return ((0.6369)*sin(sin(x))*sin(x));
}

int main()
{
  double a = 0.0;
  double b = 1.5707963267948966;
  int n = 200000;
  double h = (b-a)/(2*n);
  double s = f(a) + f(b);
  int k = 1;
  double x;

  while(k < 2*n-1)
    {
      x = a+h*k;
      s+= 4*f(x)+2*f(x+h);
      k+= 2;
    }

  cout << "integral is equal " << s*h/3;
}

With n=20 I obtain 0.412218
With n=200 I obtain 0.437438
With n=2000 I obtain 0.439964
With n=20000 I obtain 0.440216
With n=200000 I obtain 0.440241

Enjoy :)

[mike_2000_17]

@Maritimo:
Your code is wrong, see my previous post explaining why.

And secondly, as a moderator, I should point out that you should not provide complete solutions to people. People who come here with questions on problems like this one are in the process of learning to program and the problem is often about some homework assignment that they are trying to complete on their own. It does not help them to simply give them ready-made solutions. The point is to help them accomplish things on their own, and help them along by clearing some points of confusion or helping them overcome the last few hurdles.

But since you have posted complete code, but wrong code, I'm forced to post the correct code:

#include <iostream>
#include <cmath>

using namespace std;

double f(double x)
{
  return ((0.6369)*sin(sin(x))*sin(x));
}

int main()
{
  double a = 0.0;
  double b = 1.5707963267948966;
  int n = 2;
  double h = (b-a)/(2*n);
  double s = f(a) - f(b);
  int k = 1;
  double x;

  while(k <= 2*n-1)
    {
      x = a+h*k;
      s+= 4*f(x)+2*f(x+h);
      k+= 2;
    }

  cout << "integral is equal " << s*h/3;
}

Which gives output:

for n = 2:
integral is equal 0.440245
for n = 4:
integral is equal 0.440244
for n = 8:
integral is equal 0.440244
...

The first hint you should have noticed from your code is that if you need as much as 200,000 intervals to integrate a fairly smooth function with barely 6 digits of precision, then there is something seriously wrong with the code. Simpson's rule is a second-order integration method, meaning that it should generally have a quadratic convergence rate with "n" for a reasonably smooth function (when higher-order derivatives vanish quickly, as they do with sine waves, where the derivatives vanish at factorial rates). So, with n = 2, it should already be very close, and with n = 4, it should be orders of magnitude closer to the answer than at 2. And with n = 8, it should be so close that the error is buried inside the rounding-off error inherent to a fixed floating-point number type like double.

[Maritimo]

Yap, you are wright.
I wrote:

while(k < 2*n-1)

and

double s = f(a) + f(b);

Insted of:

while(k <= 2*n-1)  

and

double s = f(a) - f(b);

Sorry.

Also, in the future i´ll try not to give the complete answer.

[Auroch]

Thank you so much, guys. I think that following variant is very nice:
(Note: This is Python code)

from math import sin

def f(x):
    return ((0.6369)*sin(sin(x))*sin(x))

def method_simpson_compost(f,a,b,n):

    h  = (float(b)-a)/n
    i   = 0
    fks = 0.0
    while i<=n:
        xk = a+i*h
        if i==0 or i==n:
            fk = f(xk)
        elif i%2 == 1:
            fk = 4*f(xk)
        else:
            fk = 2*f(xk)
        fks += fk
        i += 1
    return (h/3)*fks
print method_simpson_compost(f, 0, 1.57, 10)